Smart Risk Limitation of Martingale by Logistic Growth
One of the main issues with the martingale is its inherent exponential growth. After only a few Iterations, the lot size explodes and with it the risk.
This is bad but must of the time the profits are generated in the first few iterations when the exponential growth leads to a fast exit again.
So, how to have the best of both worlds?
The answer is a function which has at first an exponential growth (like Martingale) but then transitions to a constant lot size (like grid).
Such a function exists and is well-known in nature for limited growth, the logistic function:

Naturally, L is our maxLot and k is related to the Martingale coefficient alpha by
k = ln alpha
Further, we need to define a minLot (starting Lot) and x0. x0 is just the point from which the growth will transition strongly to a constant value.
Here is an example of Martingale coefficient alpha = 1.52 compared to the logistic growth capped at a maxLot of 1.0, x0 = 11, minLot = 0.01:
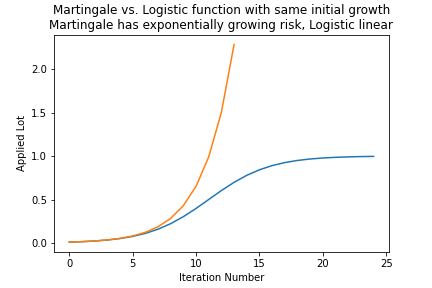
It is clearly visible how the Martingale (red line) explodes at low Iterations / cycles and with it the trade risk. The logistic function shows a linear risk increase, since the lot is constant.
I think that the logistic function gives us much more possibilities to survice strongly trending markets in which the initial trade has been in the wrong direction.
In python, the implementation of the logistic function looks as follows:
def logistic(minLot, maxLot, x0, x):
k = 1/x0*numpy.log(maxLot/minLot -1)
return maxLot/(1+numpy.exp(-k*(x-x0)))
numpy.log is the natural logarithm, in C it is
double log(double x);
Note that only x0 is a parameter that needs to be implemented in addition. minLot and maxLot are already implemented in CP, k is automatically calculated.
It would be great to have this mathematical approach implemented.
Thank you in advance!
Related suggestion: https://communitypowerea.userecho.com/en/communities/1/topics/196-max-lot-option-max-lot-per-1000




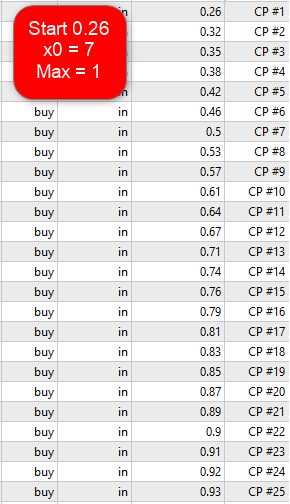
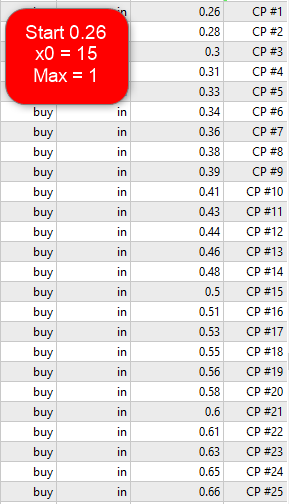



Robert, sorry for a such long delay with reply...
I've finally added this mode to the EA (will be available in v2.30).x0 is defined by "Lot coefficient / adding / x0" parameter (never mind that it is real number, just use an integer to define x0).
Max lot must be specified for this mode, of course. And now I understand why did you ask for "Max lot per 1000 USD".